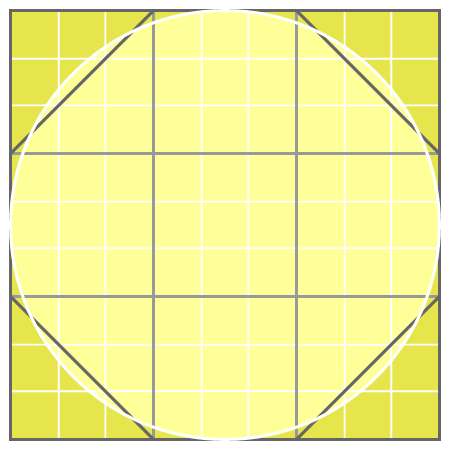
A square with inscribed circle is subdivided into parts by a grid, illustrating an ancient method of calculating a circular area by approximation. As demonstrated in the Rhind Papyrus (book II, problem 48), 1550 BC. The area of a circle is estimated as nearly 64/81 of a square, which side length equals the diameter. Using this method, the number pi is approximated by (16/9)^2 = 256/81 ≈ 3.16049, an error of only 0.01890 respectively 0.6 percent compared to π ≈ 3.14159.
Loading...